Ley de seno y coseno
a ver, en trigonometría, el teorema del seno es una relación de proporcionalidad entre las longitudes de los lados de un triángulo y los senos de los ángulos respectivamente opuestos.
sen A / a = sen B / b = sen C / c
El teorema del coseno es una generalización del teorema de Pitágoras en los triángulos no rectángulos que se utiliza, normalmente en trigonometría. El teorema relaciona un lado de un triángulo con los otros dos y con el coseno del ángulo formado por estos dos lados
c^2 = a^2 + b^2 - 2ab cos C.
sen A / a = sen B / b = sen C / c
El teorema del coseno es una generalización del teorema de Pitágoras en los triángulos no rectángulos que se utiliza, normalmente en trigonometría. El teorema relaciona un lado de un triángulo con los otros dos y con el coseno del ángulo formado por estos dos lados
c^2 = a^2 + b^2 - 2ab cos C.
Distancia entre dos puntos
Cuando los puntos se encuentran ubicados sobre el eje x o en una recta paralela a este eje, la distancia entre los puntos corresponde al valor absoluto de la diferencia de sus abscisas.
Ejemplo: La distancia entre los puntos (-4,0) y (5,0) es 4 + 5 = 9 unidades.
Cuando los puntos se encuentran ubicados sobre el eje y o en una recta paralela a este eje, la distancia entre los puntos corresponde al valor absoluto de la diferencia de sus ordenadas.
Ahora si los puntos se encuentran en cualquier lugar del sistema de coordenadas, la distancia queda determinada por la relación:

Para demostrar esta relación se deben ubicar los puntos A(x1,y1) y B(x2,y2) en el sistema de coordenadas, luego formar un triángulo rectángulo de hipotenusa AB y emplear el teorema de pitágoras.
Ejemplo: Calcula la distancia entre los puntos A(7,5) y B (4,1)
d = 5 unidades
Localización de un punto en el plano cartesiano
Como distancia a los ejes
En un plano traza dos rectas orientadas perpendiculares entre sí (ejes) —que por convenio se trazan de manera que una de ellas sea horizontal y la otra vertical—, y cada punto del plano queda unívocamente determinado por las distancias de dicho punto a cada uno de los ejes, siempre y cuando se dé también un criterio para determinar sobre qué semiplano determinado por cada una de las rectas hay que tomar esa distancia, criterio que viene dado por un signo. Ese par de números, las coordenadas, quedará representado por un par ordenado  , siendo
, siendo  la distancia a uno de los ejes (por convenio será la distancia al eje horizontal) e
la distancia a uno de los ejes (por convenio será la distancia al eje horizontal) e  la distancia al otro eje (al vertical).
la distancia al otro eje (al vertical).
 , siendo
, siendo  la distancia a uno de los ejes (por convenio será la distancia al eje horizontal) e
la distancia a uno de los ejes (por convenio será la distancia al eje horizontal) e  la distancia al otro eje (al vertical).
la distancia al otro eje (al vertical).
En la coordenada  , el signo positivo (que suele omitirse) significa que la distancia se toma hacia la derecha sobre el eje horizontal (eje de las abscisas), y el signo negativo (nunca se omite) indica que la distancia se toma hacia la izquierda. Para la coordenada
, el signo positivo (que suele omitirse) significa que la distancia se toma hacia la derecha sobre el eje horizontal (eje de las abscisas), y el signo negativo (nunca se omite) indica que la distancia se toma hacia la izquierda. Para la coordenada  , el signo positivo (también se omite) indica que la distancia se toma hacia arriba sobre el eje vertical (eje de ordenadas), tomándose hacia abajo si el signo es negativo (en ningún caso se omiten los signos negativos).
, el signo positivo (también se omite) indica que la distancia se toma hacia arriba sobre el eje vertical (eje de ordenadas), tomándose hacia abajo si el signo es negativo (en ningún caso se omiten los signos negativos).
 , el signo positivo (que suele omitirse) significa que la distancia se toma hacia la derecha sobre el eje horizontal (eje de las abscisas), y el signo negativo (nunca se omite) indica que la distancia se toma hacia la izquierda. Para la coordenada
, el signo positivo (que suele omitirse) significa que la distancia se toma hacia la derecha sobre el eje horizontal (eje de las abscisas), y el signo negativo (nunca se omite) indica que la distancia se toma hacia la izquierda. Para la coordenada  , el signo positivo (también se omite) indica que la distancia se toma hacia arriba sobre el eje vertical (eje de ordenadas), tomándose hacia abajo si el signo es negativo (en ningún caso se omiten los signos negativos).
, el signo positivo (también se omite) indica que la distancia se toma hacia arriba sobre el eje vertical (eje de ordenadas), tomándose hacia abajo si el signo es negativo (en ningún caso se omiten los signos negativos).
A la coordenada  se la suele denominar abscisa del punto, mientras que a la
se la suele denominar abscisa del punto, mientras que a la  se la denomina ordenada del punto.
se la denomina ordenada del punto.
 se la suele denominar abscisa del punto, mientras que a la
se la suele denominar abscisa del punto, mientras que a la  se la denomina ordenada del punto.
se la denomina ordenada del punto.
Los puntos del eje de abscisas tienen por lo tanto ordenada igual a  , así que serán de la forma
, así que serán de la forma  , mientras que los del eje de ordenadas tendrán abscisa igual a
, mientras que los del eje de ordenadas tendrán abscisa igual a  , por lo que serán de la forma
, por lo que serán de la forma  .
.
 , así que serán de la forma
, así que serán de la forma  , mientras que los del eje de ordenadas tendrán abscisa igual a
, mientras que los del eje de ordenadas tendrán abscisa igual a  , por lo que serán de la forma
, por lo que serán de la forma  .
.
El punto donde ambos ejes se cruzan tendrá por lo tanto distancia  a cada uno de los ejes, luego su abscisa será
a cada uno de los ejes, luego su abscisa será  y su ordenada también será
y su ordenada también será  . A este punto —el
. A este punto —el 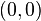 — se le denomina origen de coordenadas.
— se le denomina origen de coordenadas.
 a cada uno de los ejes, luego su abscisa será
a cada uno de los ejes, luego su abscisa será  y su ordenada también será
y su ordenada también será  . A este punto —el
. A este punto —el 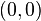 — se le denomina origen de coordenadas.
— se le denomina origen de coordenadas.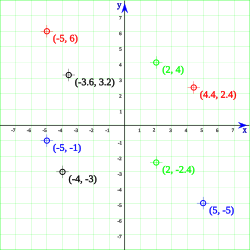
No hay comentarios:
Publicar un comentario